The index to the articles in this series is found here.

Machine learning is, as they say, a very active field. There are many ways we can go from here, and we’re likely to try a few different approaches as we explore this problem.

Now, as I’ve alluded to in previous articles, my initial thought is to make this a modular neural network. Divide the input space into separate modules that are then processed, rather than producing a network that cares intimately about the details of individual pixels. Rain far away is probably not as interesting as rain close to Ottawa, so we can use bigger buckets of points far away. I described a dartboard-like module layout. Here’s an example of what I’m thinking might work:

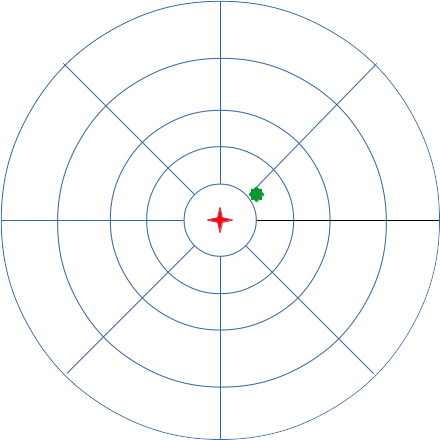
Here, the radar station is at the red star, and Ottawa is roughly on the green spot. This divides the pictures into 33 clusters.

I’d also like to add another module. I’ll call this a tripwire. It will process a ring of pixels around Ottawa, at a distance of, say, 30 pixels. Our graphs have a resolution of one kilometre per pixel, so this represents a sensitive region extending roughly an hour out of Ottawa, for moderate wind speeds. If rain starts falling in this tripwire, there’s a good chance that rain is imminent in Ottawa, and I want my neural network to pay particular attention to this condition.

These modules will do some analysis of the pixels they contain, and then will produce a set of outputs. We haven’t decided yet how many numbers will be output, we’ll experiment a bit later.

So, that’s a logical description of the layout, now to details. I’m expecting each module to involve a dense neural network of two layers. I’m not planning to make them convolutional to begin with, but might try that later, as convolutional layers might be able to distinguish incoming cold fronts, where a line of rain crosses the Ottawa Valley. In an earlier posting I dismissed the idea of using convolutional layers, but on further consideration, I’m not going to rule it out now.

Now, what about independence? Might it be possible to use a single network to process all modules in the outer ring, another for the ring inward of that, and so on? This would reduce the number of weights in our model almost eight-fold, and might therefore make the problem more tractable in terms of training time and memory consumption. This is tempting, but remember the issue with transformations that aren’t part of the symmetry group of the square grid. We have D_2 and D_4 symmetry groups available, which means that we can do rotations of 90 degrees without loss, but 45 degree rotations are a bit tricky, we lose the guarantee of 1-1 mapping, and we can’t ensure that all modules have exactly the same number of pixels in them. So, a compromise, we’ll use two independent networks per ring. Two adjacent modules will have independent neural networks, and then rotations of 90 degrees will span the entire ring. We can build a mapping of pixels to modules that guarantees identical geometries and numbers of pixels, preserving neighbour relationships.

Above these modules, I expect to have at least two more dense layers that process the inputs from the modules and compute the outputs. These layers will be relatively light-weight. If each module produces 5 outputs, and we have 34 modules, then we’ve got about 170 inputs to the synthesis layers at the top.

And, what about time dependence? I’m not thinking of using embedding at this time, where we treat the time dimension as just one more spatial dimension and so wind up with six times as many inputs and six times as many weights. I don’t really think that the output at time T+1 depends on subtle calculations of the input at pixel P1 at time T-3 and also pixel P2 at time T-1 and pixel P3 at time T, so having all that data on hand and feeding into the same network simultaneously seems undesirable.

The way I’m planning to handle the time series is with recurrent layers. I’m thinking GRU or LSTM layers, rather than simple recurrent neural network layers. My initial thought was that the recurrence would be in the modules, but I’ve changed my mind. The problem we’re trying to solve isn’t best described by the time evolution within a module (geometric sector), but the time evolution of movement between modules. So, the recurrent layer(s) would be in the synthesis layers above the modules.

Here’s a layout of the flow of data in this topology. The arrows indicate flow of information, not single values. Images are fed into the modules, and some analysis is done. The modules produce some information which is fed into one or more recurrent layers whose job it is to analyse the time-dependent behaviour of the system. This then feeds into one or more layers that roll everything up into our rain predictions.

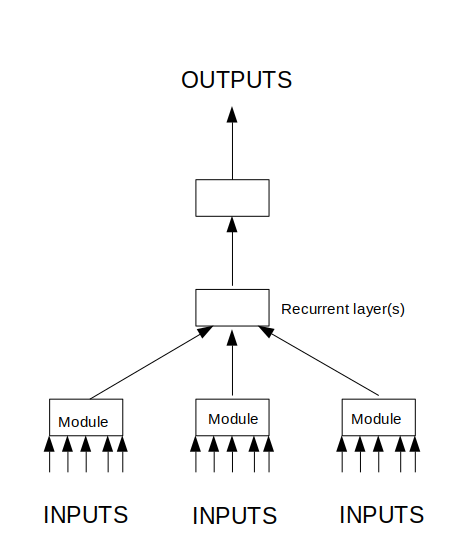
So, what I’m imagining the network is probably going to do when it has trained is that the modules will produce some sort of proxies for rain intensity, radial movement, and tangential movement of rain structures. The layer(s) above will tie together this information from different geometric sectors through time, along with the tripwire module, to produce some outputs that are related to how rain is moving through the system. The top layer(s) then produce the outputs.

In the next posting, I plan to review some terminology and approaches, for those who are not yet familiar with the details of neural network programming.

UPDATE #1 (2019-08-23): Included a link to an index of articles in this series.