The index to the articles in this series is found here.

So, I’ve got a baseline image I can use to extract active precipitation data from the government website. Now, can we just throw everything into a neural network?

The temptation is there, let the network do everything, but we have to understand our problem well enough to make sure we are using the network well. After all, neural networks turn into big black boxes, you can’t easily pull out weights one at a time and examine them to see if they look right.

Well, our time series of data for rainfall is going to have clouds moving more or less in a straight line and at a speed in the tens of kilometres per hour. Most of these events will move from roughly WSW towards ENE, but we should expect that rain might blow in from any direction. The problem is that my training set almost certainly doesn’t have any data for rain blowing in from the East. If I train with the data I have, the neural network will decide that rainfall to the East of Ottawa can never cause rainfall in Ottawa, and so input weights for pixels on that side will be zero or small. Then, when rain really does come in from there, the neural network will be surprised, and I will get wet.

It might be nice, then, to synthesize data for rain coming from the East. The most obvious way to do this is to rotate the incoming data. Note, though, that I don’t want the position of Ottawa itself to change on the plot, and the radar dish is not in Ottawa, but some distance to the South-West, in Franktown. Now, by rotating the input data we are assuming that weather patterns that approach from the East are very similar to those that approach from the West. They display a similar lack of high deflections, have similar speeds of approach, and that the unconsidered causal agents responsible for the weather (such as fronts, temperature trends, moisture loss, etc.) can be treated as symmetrical. This assumption would probably not be true for a place like Hamilton, where lake effect snows mean that precipitation to the East is qualitatively different from that to the West, or Vancouver, with a huge ocean to the West and snow-covered mountains to the East. These places don’t demonstrate the degree of rotational symmetry that we consider important for such a simple data synthesis method. Ottawa, however, far from lakes and in a large plain, with only relatively low hills in the vicinity, doesn’t have any obvious external asymmetries aside from that imposed by the prevailing winds.

If you look at the map in part 1 of this series, you’ll see that this data rotation approach on the Franktown radar station data wouldn’t work very well at all for rain in Montreal, as it is near the East edge of the imaging area, so we don’t actually have much data for rain inbound from East of Montreal. For Ottawa, though, we might be able to manage. Montreal has its own McGill radar station, so we wouldn’t be using Franktown data for Montreal in any case.

Rotations are a bit tricky on square data. We can easily rotate by steps of 90 degrees, because those operations are part of the symmetry group of the square (D_4 for all you group theory enthusiasts out there). Outside of those simple rotations, issues arise with floating-point roundoff, voids, and many-to-one mappings. If we have two adjacent pixels with value ‘3’ in the unrotated input set, and these pixels, after rotation, project partially onto four different pixels, how are we going to assign values to those pixels? The ‘3’ indicates intensity, so we don’t want to smooth it out to 1.5 on each pixel, and we’re using discrete intensities rather than continuous, so it might be awkward to try to sum up contributions on pixels in the rotated dataset. For now, we will just use the three available 90 degree rotations, as they do not distort the data, and we’ll evaluate the system’s behaviour to see if smaller rotations are necessary for good predictions.

We think, because our radar image is a disc, and rain travels more or less in straight lines, that radial movement of rain will be important. That is, rain moving toward the radar station will influence the likelihood of rain in Ottawa. Also, we’re probably not too worried about the fine details of rain falling far away, but close to Ottawa we need some finer resolution. So, let’s cut up the space a bit like a dartboard. We’ll cut the disc into a certain number of equal-width wedges, and each wedge will be cut by arcs of fixed radius. We’ll adjust the parameters of these regions to suit our model later.

So, do we centre these regions on Ottawa, or on Franktown? I’m going to centre them on the radar facility itself, because that allows for the possibility that, some time down the road, we decide to set up a system that monitors rain in two different places. We can’t centre our regions of interest on both, to do that would be just to say we’re creating two completely independent neural networks. At least to begin with, then, we’ll centre our division of the disc on the radar facility in Franktown.

Why aren’t we using convolutional neural networks? Well, that’s something we’ll keep in mind for later, but they’re the sort of thing you would use to investigate the shape of rainfall patterns within a region, and, at least for now, we think rainfall prediction is not so strongly dependent on the fine-scale features of the rainfall intensities within a region of space. So, my inputs are going to be broken into these disjoint regions, and the first layer of our network will only consider values within these regions, not between them. This is called a modular neural network. A module of neurons that look only at pixels in their area of responsibility, and feed some outputs up to the next layer for more analysis. The higher layer(s) will be able to work with outputs from multiple modules. For now, I’m not going to say how many outputs each of these first-layer regions will produce. With only one output, the network would probably train itself to something like “fraction of pixels in the region which show rain”, but it’s likely that we need a bit more information than that, so we will keep in mind the possibility that these regions will each be allowed produce multiple outputs if we decide that’s necessary. Also, the region(s) immediately around Ottawa are special. In there, we probably are interested in the fine-scale details of rainfall amounts, so we’ll either want to make those regions quite small, or we’ll want to expose those pixels separately to the higher layer of the network. It’s something to keep in mind.

OK, so that’s a basic outline of our proposed neural network topology. What about training data? We need some outcomes to validate predictions.

We’ll pick four pixels near the middle of Ottawa, and look at the rainfall in those pixels. If any pixel shows any rainfall, our real outcomes will have that bit set. If at least one pixel shows heavy rain, our real outcomes will have that other bit set. Since our bits are binned into one hour predictions and we have 6 radar images per hour, we’ll say that any rain in any one of those six radar observations will result in the corresponding bits being set.

But, as always, there are complications. Recall in the previous article that there’s a close-range phantom rainfall observed when the skies are clear and it’s humid out. Ottawa lies within this region of phantom rainfall, which means that a naive extraction would conclude that it’s almost always raining over Ottawa on muggy days. Here’s an example of such phantom rainfall:

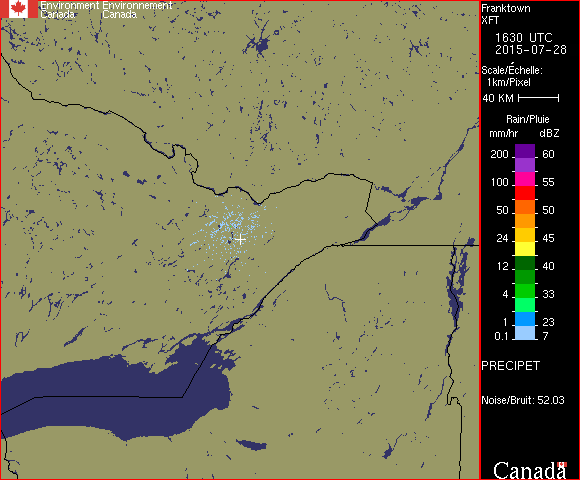
What rule are we going to use to distinguish this phantom rainfall from real rain? Well, domain knowledge time again. These regions of phantom rainfall only appear as the lightest rainfall rate, and appear as scattered pixels rather than solid regions. In real light rainfall, we always see large areas of light rain, usually with heavier rain inside. So, that’s going to be our rule. If there are only light blue active pixels within, say, 20 pixels of the radar facility, and if the density of such pixels is less than 0.5, then we’ll say that the purported rain in Ottawa is, in fact, not there. We might have to tune this condition later, but this will make a starting point.

OK, so we’ve laid out a preliminary approach. We might discover after testing that we need to do things differently, but we now have a viable first attempt.

In our next posting, we’ll process the input data to make it suitable for feeding to the neural network.

UPDATE #1 (2019-08-23): Added a link to an index page of articles in this series.