So, this is all running a bit longer than I expected when I began the series of postings. Having links to previous articles at the top of each article isn’t very clear or efficient, so here’s an index page I’ll update as new postings are added.
- Introduction to the problem. I describe what problem I’m trying to solve, give an example of the data that will be used to train, and lay out a rough sketch of where I’m going with this project.
- Preparing baseline data. I show how I produce a single rain-free image that will be used as a baseline subtraction so that I can extract only rain-related pixels, without cluttering my data with local geography.
- Domain knowledge. I discuss the form of the data, its known characteristics, and how I think this will influence the design and topology of the neural network. I also discuss the possibility of generating synthetic data by rotations, to handle the rare, but possible cases of rain coming from the East. I explain why those rotations might be useful in the case of Ottawa, but in certain other cities, local geography would make such operations less valuable.
- Extracting rain information. Here I provide the code that converts the raw .gif files downloaded from Environment Canada into an intermediate binary representation of my own design, in which only actual rainfall intensities appear.
- Building data for single images. Here, I provide code that reads this intermediate binary representation and decides whether a particular image indicates rainfall present in Ottawa at that moment. The code also computes a sequence number, an integer which will differ by one between two radar images that were taken 10 minutes apart.
- Locating training candidates. Our neural network is a predictive model, it has to be trained on continuous runs of images. The ‘true’ values against which we will be computing errors and training the network are, themselves, a function of multiple input files. We sometimes have missing files due to radar downtime, network disconnects on my home machine, or delays in the .gif files being made available on the Environment Canada website. In this article I show how complete continuous runs of images are located and the true values extracted, then all this information is stored in a single record for later use.
- Github sources. With all the source files I’ve been supplying, and as I started to patch them, it becomes necessary to provide a more convenient way for readers to examine these files. This article describes the github archive, and how to locate it.
- Thinning the data. Some of our training candidates are uninteresting. Clear skies to the radar horizon producing no rain is something that we want in the training set, but we don’t need a thousand or more examples of that. Categorical neural networks train best on balanced training sets, where positive and negative outcomes are roughly equal. I go over this here.
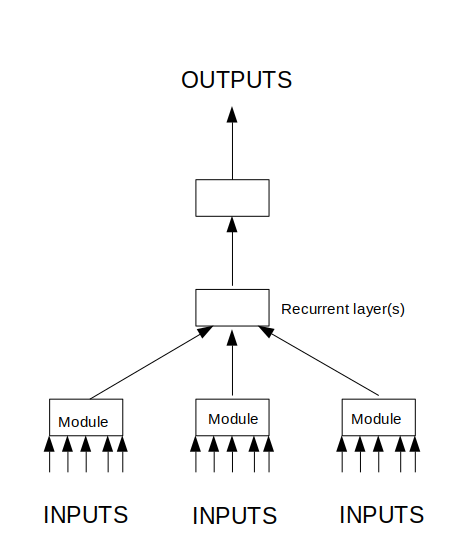
- Neural network logical design. Here I use diagrams to show how the training data is interpreted in two-dimensional space, and how the neural network is to be laid out to process this.
- Terms and definitions. I decided that I was using a lot of technical terms without providing much context, and interested readers might be getting lost in some of the jargon, so I provided a very brief overview of terms specifically related to what I’ve been discussing in this series of postings. This is not an exhaustive overview of the terminology of neural networks.
- Basic Keras code. At last, I show you a python script that invokes Keras code. This is just a toy example, there to experiment with syntax, but it encapsulates all of the features that are neither obvious nor trivial in a short snippet for readability.
- Data discussion. Before training the network, I take an aside to discuss data and our training parameters. I also split the set of candidates into training and validation groups.
- The data generator. A short review of the code I’m using to feed training data into Keras. It allows Keras to load batches, subsets of the training set, and adjusting the weights after each batch as it walks through the training set.
- Training the model. So, now I can feed the data in and train the model. It’s straining the hardware of my machine, so we discuss next steps, how to make the model more compact.
- Coarse-scaling the model. The first neural network training attempt failed because our model was simply much too big. Even if the memory had been sufficient to run to completion, the training time was impractical. So, the next thing to try was to coarse-scale the data. This covers that approach.
- Observations from the coarse-scaling. I go over the results of the changes to the network, and describe the next approach I plan to take, which will greatly simplify the neural network.
- Preprocessing the data. It turns out that we now have a bottleneck in the conversion of raw data to inputs suitable for the neural network in the new topology. So, I’ve changed the preprocessor to compute input vectors and save them in the intermediate binary files.
- Performance improvements. I discuss the impact of the changes that I’ve made over the course of this project, and where we go next.
- Preparing to tune. I present the current state of the training code, and discuss how we’re going to be tuning the network.
- The holdout dataset. I discuss another dataset, and how we’ll be evaluating the usefulness of our model.
- Initial tuning of the network. I plot some graphs to show the effect of different optimizers and batch sizes.
- Overfitting and the Adagad optimizer. A short post to show a very clear example of network overfitting.
- Results of first experiments.
We review the performance of our different optimizers in the first run of experiments. We decide that we need to re-run these experiments, and that we’ll also want to put in regularizers.A data formatting error invalidates these results. - Preparing for regularization.
I discuss the objective and methods of regularization that I intend to investigate for this project. We’re preparing to use TensorBoard.A data formatting error invalidates these results. - Analysing the weights.
I put up some histograms of the weights and talk about what we can conclude from them.A data formatting error invalidates these results. - Found an error in the inputs. The recent analysis is invalidated due to a software bug. I have to start over.
- Repeat runs. I repeat the experiment runs, and get somewhat disappointing accuracy. Then I look at the failed predictions, and realize the training data is wrong, and the network is right.
- Success. The network now performs as well or better than I can by looking at the same images. I’ll be tweaking and experimenting with the aim of reducing incorrect predictions.
- Followup experiments. I tried to improve the discrimination of the model with a few network tweaks, but nothing really made a difference.
- Graphical widget. A little graphical widget now sits on my screen, giving me rain predictions at a glance.
- Summary of project. The project is essentially complete. I describe what I’ll be doing in future, and may write followup posts if something interesting comes up.
- More data. I’ve downloaded more training data. Discuss some obstacles, and future directions.
- Results with more data. Did some training with the larger dataset. It revealed problems in the earlier approach, and forces me to revisit some ideas.
- A data problem is found. I figure out why the larger training set is behaving so strangel
- New features. I’m still experimenting to find good features for the rain prediction network.
- Final thoughts. The project is complete, and working well. Thank you for your attention. This has been a very long series!